이번 포스팅에서는 Finite Quantum Well (FQW)의 여러 버전들을 살펴볼 것이다.
첫 번째로 살펴 볼 것은 Single quantum well (SQW)을 다시 한 번 볼 것이다.
이전 포스팅에서 가져온 것은 Wikibooks 출처라 내가 보이고 싶은 것을 보이지 못했다.
우선 현실적으로 QW system은 반도체를 Hetero structure로 하여 만들기 때문에
현실적으로 갖는 Barrier와 Well potential energy 차이는 0.5~1 eV 정도이다.
이 계산에서는 Well과 Barrier의 전자 유효질량은 고려하지 않을 것이다.
Potential energy 차이는 0.5 eV로 고정 시켜서 계산했다.

위 그림은 SQW system에서 Bound states의 전자 확률 분포를 나타낸다.
quantum number (n)가 증가할 수록 (Energy level이 높아질 수록) Bound state의 Barrier 전자 확률 분포는 증가한다. 또한 node의 개수 또한 증가한다.
Potential 구조가 대칭적이기 때문에 파동함수는 even과 odd mode가 교대로 나오고 있다.
Energy level이 증가하다가 n =5 를 벗어나면 Scattering state (n = 6)가 되고 전자 확률 분포는 Well & Barrier 전역에 분포한다.
자연은 에너지 레벨이 낮은 것 부터 채우려는 경향이 있다.
따라서, Ground state에 있는 전자 개수는 가장 많을 것이다.
그렇지만, 이런 것을 고려하지 말고 Bound states에 균등하게 전자가 있다고 생각해보자.
그렇다면, SQW System에서 각 상태에 전자를 발견할 확률은 균등할 것이다.
각 quantum number에 대응하는 파동함수들은 system을 설명하는 basis가 된다.
따라서, 다음의 식으로 SQW system을 설명할 수 있다.
$$ \Psi(x) = \frac{1}{\sqrt{5}}(\sum_{n=1}^5\psi_n(x))$$
이 파동함수의 절대값의 제곱을 한 형태를 Graph로 나타내면 다음과 같다.

전자 확률 분포는 Well을 중심으로 대칭적으로 존재하지 않고 Well 영역에만 분포하지 않고
Barrier에도 약간이지만 분포하고 있다.
Tunneling으로 인하여 FQW system에서는 Barrier에도 확률 분포가 있음을 알게되었다.
그렇다면, SQW 두 개를 붙여놓은 Double quantum well (DQW)는 어떨까?
먼저 가운데에 Barrier를 20 nm 깔아놓고 계산을 수행했다.

가운데 Barrier가 20 nm로 두껍게 쌓아놓으니 두 개의 SQW는 독립적으로 확률 분포가 생겨난다.
이러한 System을 우리는 Multiple quantum well (MQW) system이라고 부른다.
보통 QW 소자는 Laser 같은 광소자로 응용되곤 한다. SQW 소자로는 우리가 원하는 광세기를 낼 수 없기 때문에 이런 식으로 여러개의 SQW을 쌓은 MQW를 사용하여 효율을 높인다.
그러면 가운데 Barrier 폭을 10 nm로 좁혀보자.

아직 까지 서로 독립된 states로 존재하고 있는 MQW system이다.
좀 더 줄여서 5 nm로 줄여보자.

가운데 있는 Barrier 폭을 5 nm로 줄이니까 왼쪽에 있는 SQW의 전자 확률 분포가 더이상
왼쪽에만 존재하지 않고 오른쪽에도 약간 존재한다. (Blue line과 Magenta line)
이것은 왼쪽의 SQW에 있는 전자가 Tunneling을 통해 오른쪽 SQW로 갈 수 있음을 의미한다.
이 현상은 에너지 레벨이 올라갈 수록 Tunneling을 통해 이동하는 전자 확률 분포가 증가한다.
(Cyan line과 Yellow line)
가운데 Barrier 폭을 좀 더 줄이면 위에서 일어난 현상은 더 잘 일어날 것 같다.
2 nm까지 감소시켜 계산을 수행한 결과는 다음과 같다.
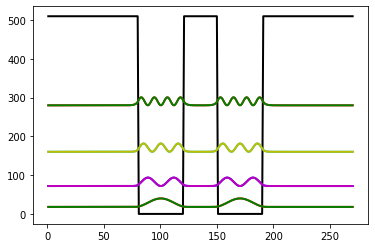
2 nm 까지 감소시키니까 전자 확률 분포는 왼쪽과 오른쪽에 균등하게 분포한다.
이 정도까지 감소시키면 MQW로서 광소자의 광 효율을 증가시킬 수 없다.
현재도 Potential 구조가 대칭적이기 때문에 even mode와 odd mode가 교대로 나오는 것을 확인할 수 있다.
이제 Potential 함수의 구조의 대칭성을 깨보자.
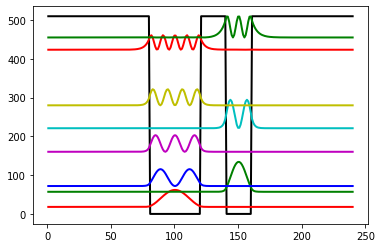
Potential 구조가 비대칭적이기 때문에 파동함수들은 even mode와 odd mode가 교대로 나오지 않는다.
Eigenenergy 또한 왼쪽과 오른쪽에서 따로 생기는 것 처럼 보인다.
이러한 비대칭적 DQW을 사용하면 다양한 광소자 등을 제작할 수 있다.
이런식으로 얇은 Barrier를 가진 QW을 쌓아가면 독창적인 특성을 가진 레이저, photo detector 등을 만들 수 있다.
'Physics > Quantum Physics' 카테고리의 다른 글
| Harmonic Oscillator (0) | 2022.08.14 |
|---|---|
| Finite potential well (0) | 2022.08.04 |
| Infinite potential well system (0) | 2022.07.24 |
| Schrodinger Equation (0) | 2022.07.21 |
| History of Quantum Mechanics (0) | 2022.07.18 |




댓글