지난 포스팅에서 Infinite potential well에 대하여 정리했다.
Infinite potential well은 양자역학 시스템에서 가장 단순하게 해석적 수식을 얻을 수 있는 예제였다.
하지만, 실제로 연구나 산업계에서 많이 사용되는 구조는 Finite potential well 구조이다.
Finite quantum well 구조 (= FQW) 실용적인 양자역학 시스템으로
광소자 등으로 많이 사용되고 있다.
FQW 부분은 2개의 포스팅으로 나누려고 한다.
첫 번째는 FQW에서 Solution들을 구해보고 여기서 우리가 해석할 수 있는 것을 정리하려고 한다.
두 번째는 single quantum well 구조를 넘어서 symmetric double quantum well (SDQW)과
asymmetric double quantum well (ADQW)에서 파동함수와 고유에너지를 계산해볼 것이다.
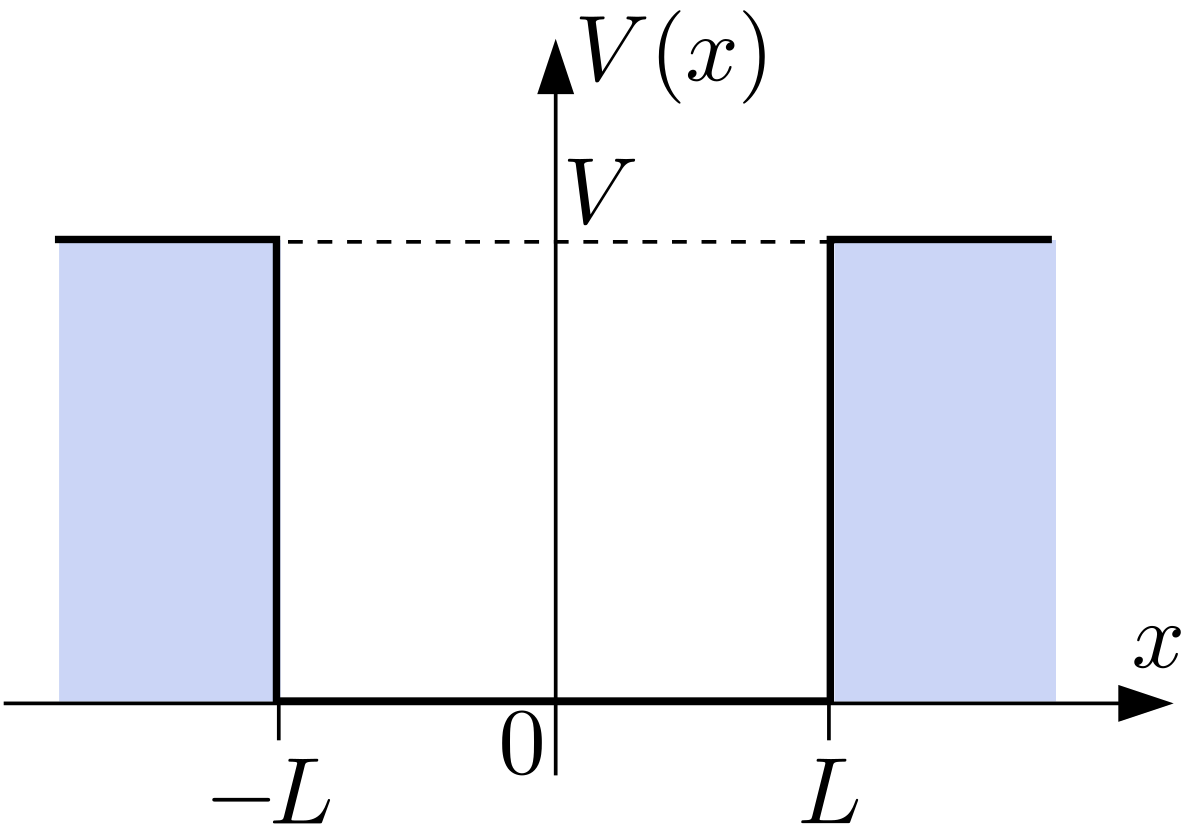
위의 그림이 나타내는 시스템이 FQW 구조로 Well이 하나 있기 때문에 Single quantum well (SQW) 이라고 부르기도 한다.
여기서, Well 영역은
이제 미시세계를 지배하는 Schrodinger equation을 생각하자.
이전 Infinite potential well에서는
그래서, 이전과 달리 Schrodinger equation을 한 번에 풀 수 없다.
이런 SQW 구조를 푸는 기본적인 전략은 아래와 같다.
1.
2. 각 영역에 Schrodinger equation의 해를 뽑는다.
3. 경계조건을 통해서 연결시킨다.
1. V(x)
1)
2)
3)
2. Schrodinger equation의 해
1) 영역과 3) 영역에서 Schrodinger equation을 보자.
(주의 : 현재 우리가 구하려는 state는 Bound state이기 때문에
고려하는 eigenenergy는
위의 미분 방정식을 만족하는 해는 exponential의 선형결합이다.
2) 영역에서는 단순하다.
위의 식의 해는 삼각함수의 선형결합이다.
3. 경계 조건
우선 우리가 고려할 경계 조건은 3가지다.
1 :
2 : 경계면에서
3 : 경계면에서
1 조건은 우리가 고려하고 있는 전자의 파동함수의 절대값 제곱이 확률 분포를 만족해야 하니
정규화를 위해 가져야 한다.
2 조건도 경계면에서 연속인 것 또한 합리적이다.
3 조건의 경우 다음의 관계를 통해 유도된다.
위의 식에 경계면 근방에서 적분을 취해보자.
1 조건으로 인하여
2와 3 조건을 적용하기 전에 문제의 상황을 단순하게 풀어내기 위하여 System을 분석하자.
SQW system은 infinite potential well과 같이 potential function이 x = 0에 대하여 대칭적인 구조를 가진다.
따라서, solution이 되는 함수는 even function과 odd function이 교대로 나올 것이다.
먼저 even function을 고려하자.
그러면,
이제 2 조건과 3 조건을 적용하면 다음의 두 개 식을 얻을 수 있다.
위의 두 식을 나누고 정리하면 다음과 같이 정리할 수 있다.
이제
이제 위의 관계를
위와 같이 정리된다.
즉, SQW 구조에서 even mode의 해를 구하기 위해서는 위와 같은 transcendental equation을 풀어야한다.
그리고 odd mode 또한 상황은 같다. odd mode를 구하는 transcendental equation은 아래와 같다.
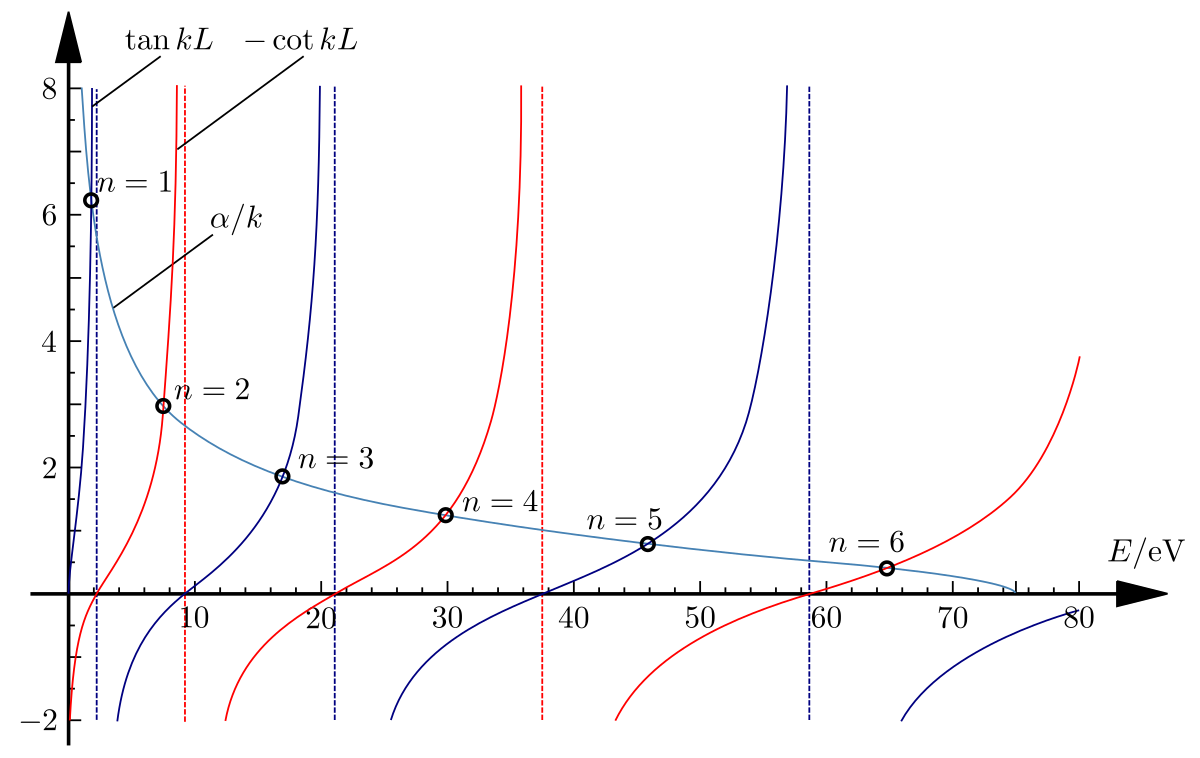
위의 transcendental equation을 plot하면 다음과 같다.
이 부분은 직접 만들려 했으나 시각화가 도저히 예쁘게 되지 않아서 Wikibooks에 이미지를 가져왔다.
하늘색 선과의 교점은 o marker로 표시가 되어있다.
하늘색 선과 파란 선의 교점은 even mode를 나타내고 붉은 색 선과의 교점은 odd mode를 나타낸다.
그리고 각 해가 되는 지점들에서 z를 알 수 있고 이를 통해 wave number인 k, l을 알 수 있다.
그러면, SQW system에서 Eigenenergy와 wavefunction을 구할 수 있다.
아래 그림은 SQW system에서 Eigenenergy들을 나타낸다.
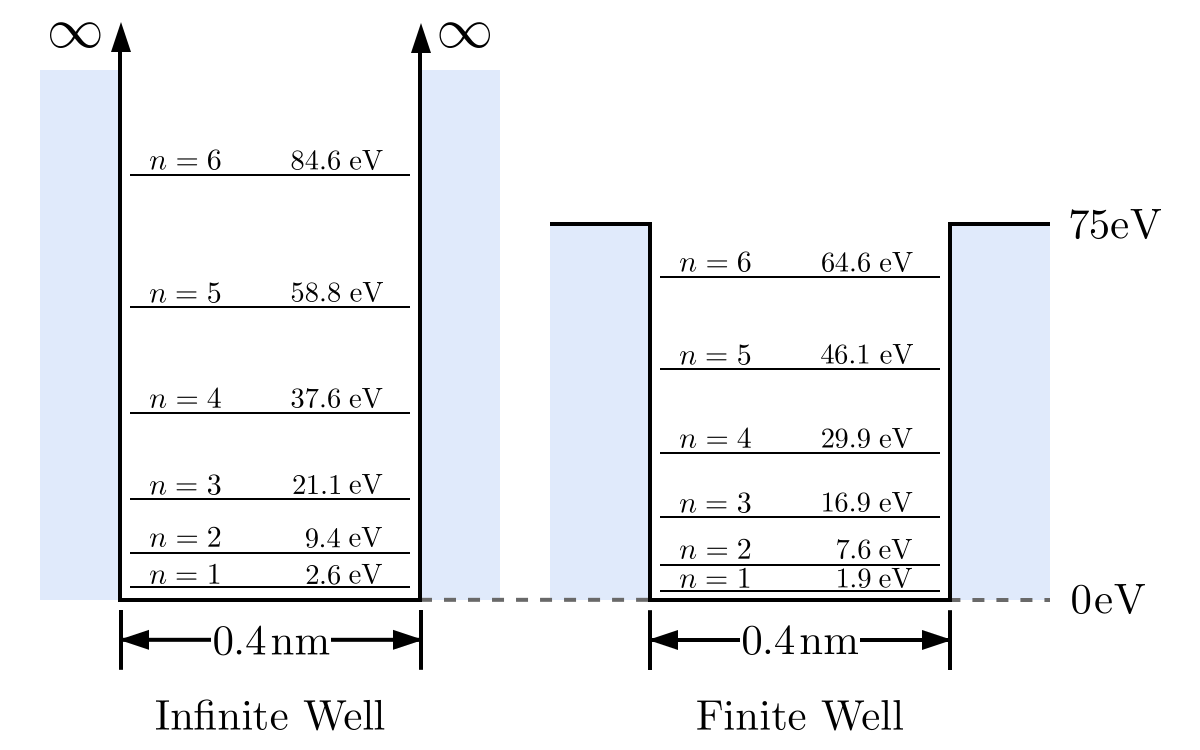
여기서 n은 Infinite well과 같이 quantum number를 나타낸다. n이 증가할 수록 Eigenenergy가 증가하는 것을 볼 수 있다.
현재 Barrier와 Well의 potential energy 차이는 75 eV로 큰 차이를 보인다.
사실 이 정도의 에너지 차이면 Well에 있는 입자 입장에서 Infinite potential로 보일 것이다.
그러나, 실제로 두 시스템에서 Eigenenergy에서 차이를 보이는 것을 확인할 수 있다.
이것은 Finite potential이기 때문에 생기는 변화이다.
만약 Potential energy 차이를 고정시키고 Well의 폭을 증가시킨다면 두 시스템은 서로 근사를 할 것이다.
왜냐하면 Well width가 좁을 수록 Eigenenergy가 가파르게 증가한다.
(우리는 이런 현상을 Infinite potential system을 공부하며 확인했다.)
0.4nm system은 매우 좁은 well 폭이기 때문에 75 eV Barrier에서도 6개의 bound state 밖에 생기지 않는 것이다.
반대로 Well 폭을 넓히면, 전자 분포가 Well에 더 많이 분포할 수 있고 이 상황은 Infinite potential well과 유사해져
두 시스템은 근사됨으로 Eigenenergy는 서로 근사할 것이다.
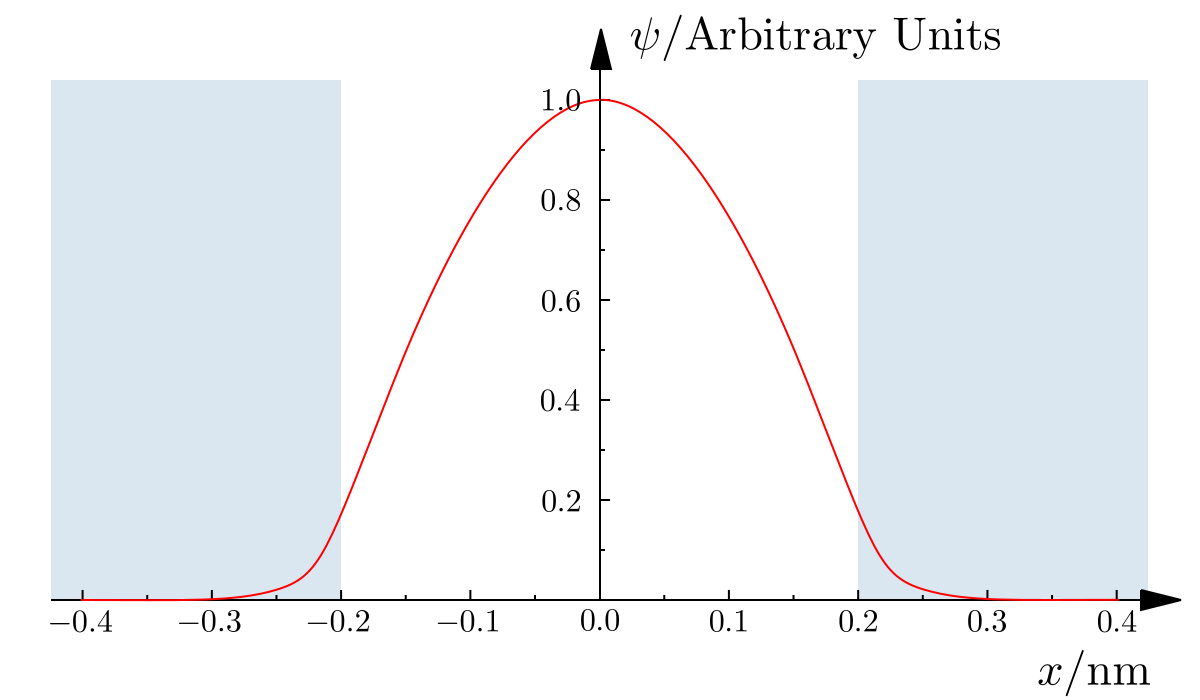
이제 SQW에서 파동함수를 보자.
위는 n = 1 (ground state)에서 전자 파동함수이다.
Infinite potential에서와 가장 큰 차이는 Barrier 영역에서 전자 확률 분포가 존재하는 것이다.
사실, 이런 현상은 고전물리에서 등장할 수 없는 현상이다.
왜냐하면 우리는 벽에 부딪혀 다른 곳으로 튕겨 나가지만, 벽 속에 들어갈 수 없기 때문이다.
이러한 Barrier에서 전자가 존재하는 확률 분포를 Tunneling이라고 부른다.
물론 Tunneling은 이런 의미 보다는 전자가 Barrier를 뚫고 다른 영역으로 이동할 때 많이 사용된다.
다음 포스팅에서는 이런 Tunneling이 어떤식으로 발생한느지 알아 볼 것이다.
위는 n = 2 (first excited state)에서 전자 파동함수이다.
여기서 볼 것은 node가 n = 1에서 보다 한 개 증가했다는 것이다.
이를 통해 n이 한 개 증가할 때마다 node 개수가 증가할 것을 예측할 수 있다.
n = 2의 Barrier 전자 확률 분포는 n = 1의 것보다 많은 것을 확인할 수 있다.
이것의 이유를 설명하자면 n = 2의 Eigenenergy는 7.6 eV, n = 1의 Eigenenergy는 1.9 eV로 n = 2의 상태가
높은 에너지에 있다.
따라서, 높은 에너지 상태에있는 전자는 Barrier로 Tunnealing 확률이 높아진다.
n이 증가할 수록 Barrier에 존재하는 전자 확률 분포는 증가하고 Bound state를 벗어나 scattering state (여기서는 n > 6)가 되면 전역에 전자 확률 분포가 생긴다.
'Physics > Quantum Physics' 카테고리의 다른 글
| Harmonic Oscillator (0) | 2022.08.14 |
|---|---|
| Finite Quantum Well 2 (0) | 2022.08.14 |
| Infinite potential well system (0) | 2022.07.24 |
| Schrodinger Equation (0) | 2022.07.21 |
| History of Quantum Mechanics (0) | 2022.07.18 |





댓글