양자역학이 어떻게 정립되었는지 흐름을 아는 것은 중요하다.
흐름을 알면, 왜 이런 생각들이 나왔는지 알 수 있기 때문에 공부를 하거나 연구를 할 때 중요한 부분이 된다.
하지만, 교과서에는 이미 확립된 내용을 다루기 때문에 이런 흐름을 잡는 것은 약간 부족할지도 모른다.
따라서, 이번 게시글에서는 양자역학에서 일어나 굵직한 역사들을 짧게 정리하고자 한다.
양자역학의 시작을 말하기에 앞서, 먼저 빛을 알아야한다.
과거 빛은 논쟁의 대상이었다.
빛이 파동인지 입자인지에 대한 과학자들의 견해는 모아지지 않았다.
빛이 입자라는 주장을 한 사람 중 대표는 Newton
빛이 파동이라고 주장한 사람 중 대표는 Huygens였다.
그러던 중, 대립된 의견을 결정지을 실험이 19세기 초에 나타났다.
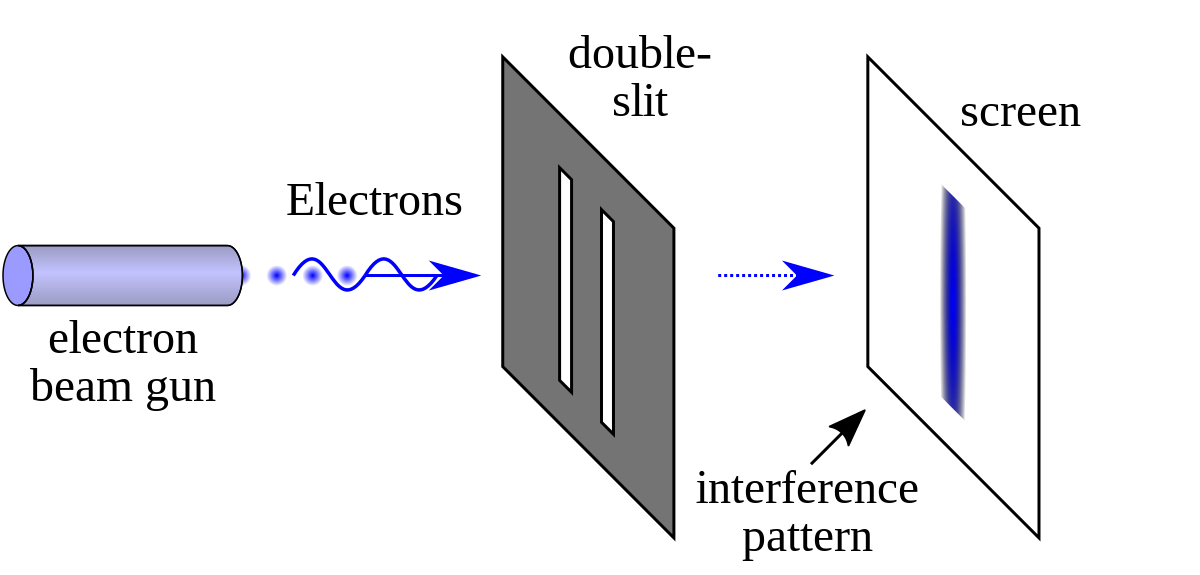
'Young's double slit experiment'
Young의 실험은 간단했지만 대상이 입자성을 가지는지 파동성을 가지는지 증명하기에 충분했다.
단지, 이중 슬릿에 빛을 쏴서 Screen에 도달한 빛의 패턴을 보면 되는 것이다.
빛이 파동이라면 간섭, 회절과 같은 성질을 가지고 있을 거 니까 회절무늬가 발생할 것이고
입자라면 나타나지 않을 것이다.
당시에 실험 결과는 Huygens 학파의 의견에 손을 들어주었다.
19세기에 Maxwell은 전기장과 자기장이 서로 연관되어 있음을 Maxwell's equation을 통해 정립했다.
이때, Maxwell은 전자기파의 속도가 광속과 유사함을 발견하였다.
이를 통해서 Maxwell은 빛은 전자기파이며 파장을 여러개 가진다는 사실을 발표했다.
이렇게, 빛이 파동이라는 것에 이견은 없는 것 처럼 보였다.
하지만, 19세기 말, 당시 과학자들은 주어진 온도에서 열에너지 복사가 어떻게 진행되는지
이론적으로 설명하고 싶어했다.
그래서, 복사를 완전히 흡수하거나 방출하는 'Black body'라는 이상적 물체를 설정했다.
Black body radiation을 설명하기 위해 여러 과학자들이 달려들었다.
Wien의 결과는 high frequency에서 잘 맞았고 다른 곳에서는 맞지 않았다.
여기에는 이론적 틀 없이 그저 숫자로 저글링을 한 결과였기 때문일 것이다.
Max Planck도 Black body radiation을 설명하기 위해 노력했던 사람이었다.
하지만, 그가 어떤식으로 접근해도 설명하기는 어려웠었다.
Planck는 수 많은 좌절 끝에 Boltzmann이 연구하던 통계역학의 기본적인 아이디어를 이용해보기로 결정한다.
당시, 학계 분위기는 통계역학을 인정하지 않았었다.
왜냐하면, 그들에게 물리학은 하나의 방정식으로 자연을 기술할 수 있어야 했기 때문이다.
여기서, Planck가 얼마나 이 문제에 간절했는지 알 수 있다.
그렇게, Planck는 에너지가 정수배로 존재한다는 아이디어를 이용해 풀어보니 Black body radiation의 이론 결과가
실험 결과와 아주 잘 맞는 결과를 얻게된다.
그리고 그는 이 내용을 1900년에 논문으로 발표한다.하지만, Planck는 자신이 사용한 양자화가 어떤 의미를 가지는지 자신도 몰랐었다.
그의 양자화와 관련된 해석을 한 과학자는 1905년에 5편의 논문을 발표했던 Einstein이었다.
Einstein은 Planck의 양자설을 받아들이고 광양자설을 제안한다.
빛은 파동적 성질과 입자 성질을 가지는 이중성을 가지기 때문에 빛의 에너지도 빛의 주파수에 비례한다고 생각했다.
이렇게 설명하니까, 특정 주파수 이상의 빛을 금속에 조사시에 전자가 튀어나오는 이른바 광전효과가 설명이 되었다.
이후로 양자역학이 발전하게 되었다.
Bohr의 원자모형을 발표, Pauli의 Exclusion principle, Heigenberg의 행렬 역학 등 여러 이론적 논의가 나타났다.
1925년에는 de Brogile의 Matter Wave를 발표했다.
Matter wave는 내용이 굉장히 재미있다.
Momentum이라는 것은 고전역학에서 다음의 수식으로 정의했다.
$$p = mv$$
질량을 가진 입자라면 위의 식으로 momentum 정보를 알 수 있다.
하지만, 파동에 대한 운동량은 알 수 없었다..
de Brogile는 Einstein의 빛이 입자로도 해석이 된다면 파동도 운동량을 가져야 한다고 생각했고
다음의 식으로 파동 또한 운동량을 가진다고 주장했다.
$$ p = \frac{h}{\lambda}= \hbar k$$
여기서 h는 Planck's constant이고 \(\hbar\)는 Reduced Planck's constat
\(\lambda\)는 파동의 파장이고 k는 wave vector이다.
이 이론은 1927년 Davisson & Germer에 의해 실험적으로 검증이 됐다.
당시 그들은 전자가 파동적 성질을 가짐을 실험적으로 보였다.
다시 말해서, de Brogile의 Matter's wave가 말해주는 것은
'파동도 운동량을 가지며 입자도 파장을 가진다.
즉, 입자는 파동으로도 해석될 수 있고 파동은 입자로도 해석이 될 수 있다.' 이다.
즉, Wave-Partice duality를 의미한다.
이를 통해, 입자의 파동함수를 구할 수 있으면 미시세계에서 입자의 상태를 해석할 수 있다는 사실을 알게 되었다.
de Brogile의 matter wave가 발표되고 다음 해인 1926년에 Schrodinger의 Wave equation이 발표된다.
당시, 양자역학을 기술하던 Heigenberg의 행렬역학은 양자역학을 잘 기술할 수 있었으나
수학적으로 복잡하다는 단점을 가지고 있었다.
반면, Schrodinger equation은 수식도 깔끔하며 이론적으로도 완벽했다.
하지만, 문제가 있었다.
전자의 파동함수는 Schrodinger equation을 통해서 얻을 수 있지만
전자의 파동함수가 무엇을 의미하는지 알 수 없었다.
이 문제를 해결할 실마리를 준 것은 1927년 Born의 파동함수에 대한 해석이었다.
그의 해석은 \(\psi\)의 절대값의 제곱을 한다면 그 함수의 의미는 전자를 발견할 확률밀도가 된다는 것이었다.
따라서, 전자가 어디에 있는가? 와 같은 질문을 이제 던질 수 없다.
그저 확률적으로만 얘기할 수 있다.
'Physics > Quantum Physics' 카테고리의 다른 글
| Finite Quantum Well 2 (0) | 2022.08.14 |
|---|---|
| Finite potential well (0) | 2022.08.04 |
| Infinite potential well system (0) | 2022.07.24 |
| Schrodinger Equation (0) | 2022.07.21 |
| 양자역학 공부 시작! (0) | 2020.02.28 |






댓글