앞으로 기술할 입자는 전자로 제한하여 설명하겠다.
운동 에너지와 포텐셜 에너지만이 포함된 Schrodinger equation은 다음처럼 기술된다.
$$ i \hbar \frac{d\Psi}{dt} = -\frac{\hbar^2}{2m} \nabla^2 \Psi +V \Psi $$
이런 Schrodinger equation을 time dependent Schrodinger equation (TDSE)이라고 부르는데, x, y, z, t에 대한 4차원의 미분방정식이된다.
풀기 매우 복잡한 형태라는 것이 한 눈에 보이기 때문에, 물리적인 상황을 좀더 고려해서 단순화시킬 필요가 있다.
포텐셜 에너지의 경우 일반적으로 공간에 대한 의존성을 가진다.
다시 말해서, 포텐셜 에너지는 시간에 대한 의존성을 갖지 않은 System을 주로 해석한다.
(하지만, 실제로 포텐셜 에너지에 시간에 대한 의존성을 가질 때가 있다. 이런 경우는 시간에 대한 포텐셜 에너지를 분리하여 Time dependent perturbation theory를 이용하여 분석한다.)
포텐셜 에너지가 공간에 대한 의존성을 가지는 경우는 다음처럼 표현한다.
$$V(x, y, z, t) = V(x, y, z)$$
이 경우 TDSE의 파동함수(\(\Psi\))를 공간과 시간에 대한 변수 분리를 행할 수 있다.
$$\Psi(x, y, z, t) = \psi(x, y, z) f(t) $$
그러면, 좌측 항과 우측 항은 변수 분리 상수를 기준으로 분리할 수 있고 다음의 두개 방정식으로 나뉘어 진다.
그리고 물리적으로 좀 더 단순한 상황을 해석하기 위하여, 1차원인 상황을 고려하기로 한다.
$$-\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2}+V(x)\psi(x) = E\psi(x) $$
$$ \frac{df}{dt} = \frac{E}{i\hbar} f$$
위의 미분방정식은 공간에 대한 의존성만 가지기 때문에, Time independent Schrodinger equation (TISE)라고 부른다.
아래의 미분 방정식은 파동함수에 시간에 대한 움직임 (evolution)을 기술하는데, Solution은 쉽게 찾을 수 있다. (\(E = \hbar \omega\))
$$f(t) = f_0 exp(-\frac{E}{i\hbar}t)$$
$$ = f_0 exp(i\omega t)$$
파동함수의 시간에 대한 의존성은 특정 주파수를 가진채로 evolution한다.
이번 포스팅에서는 TISE를 infinite potential well system에서 풀어보려고 한다.
들어가기에 앞서서, 왜 infinite potential well이 중요한지에 대하여 나의 생각을 정리하려고 한다.
1) Infinite potential well은 풀기 정말 쉬운 system이기 때문에 양자역학을 처음 공부하는 사람에게 좋은 예제가 된다.
2) 간단한 예제이지만, 많은 insights을 우리에게 알려준다.
3) 나중에 Quantum well과 같은 system으로 갈 때 활용할 수 있는 것들이 많이 있다.
Infinite potential well은 Schrodinger equation을 풀기에 쉬운 System이다.
위의 그림에서 확인할 수 있는 것 처럼, 풀고자 하는 공간 domain이 \(x \in [0, L]\)이고 여기서 포텐셜 함수는 0이다.
그 외에 영역에서 무한 포텐셜을 가진다.
infinite potential인 영역에서 입자가 존재할 확률은 0일 것이다.
따라서 경계조건으로 \(\psi(0) = \psi(L) = 0\)이 생긴다.
Infinite potential well이 주는 첫 번째 insight는 infinite potential 영역에서 입자는 존재하지 않는다는 것이다.
여기서 우리가 풀고자 하는 TISE는 다음과 같이 변한다.
$$-\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2} = E\psi(x), x \in [0, L]$$
그러면, 이차 미분방정식을 풀면된다.
공학수학에서 배운 지식을 쓰면 위의 방정식에 해는 sin함수와 cos함수의 선형결합으로 표현되는 것을 알 수 있다.
그 다음, 경계조건을 만족시키면 된다.
이 과정에서 식을 단순하게 표현하기 위해서, \(k = \frac{\sqrt{2mE}}{\hbar}\)로 썼다.
일단 \(\psi(0) = 0\) 조건만 만족시킨 Solution은 다음과 같다.
$$\psi(x) = A sin (kx)$$
\(\psi(L) = 0\)을 집어 넣으면 \(kL = n\pi\)라는 조건이 생긴다.
이게 무슨 말이냐 하면 위의 경계조건을 만족하는 해는 유일하지 않고 여러개 존재한다는 말이다.
왜 이런일이 발생할 수 있냐하면, 변수 분리 상수 E가 유일할 것이라는 보장이 애초에 없기 때문이다.
여기서 변수 분리 상수 E는 사실 에너지를 의미하는데 infinite potential well system에 있는 전자는 여러 에너지 상태로 존재할 수 있음을 의미한다.
다시 돌아와서, \(k_n = \frac{n\pi}{L}\) 로 정리할 수 있고 n에 따라서 k가 결정된다.
이 말은 곧 n에 따라서 에너지와 파동함수가 결정된다.
$$E_n = \frac{\hbar^2 \pi^2}{2mL^2} n^2$$
$$\psi_n(x) = A sin(\frac{n\pi x}{L})$$
이렇게 n에 따라서 물리적 상태와 에너지가 결정되는데 이러한 정수를 qunatum number라고 부른다.
quantum number는 물리적인 상태를 잘 나타내는 변수가 되기 때문에 양자 물리학 기술을 한층 편하게 만든다.
이런 quantum number를 메인 변수로 하여 Dirac notation을 사용하면 기술이 매우 편리해지는데 이건 다음에 제대로 도입하겠다.
이제, A를 처리해보자.
우리는 파동함수는 의미를 가지지 않고 파동함수의 절댓값의 제곱이 확률 밀도를 의미하는 것을 알고 있다.
따라서, \(\int {|\psi_n(x)|^2}dx = 1\)을 만족시키는 Normalization을 한 번 거쳐야한다.
Sin 함수는 orthogonality가 잘 알려져 있어서 \(A = \sqrt{\frac{2}{L}}\)로 쉽게 결정된다.
$$\psi_n(x) = \sqrt{\frac{2}{L}} sin(\frac{n\pi x}{L})$$
물리적 해석은 해당 결과들을 시각화하고 논하기로 하자.
Result
해당 결과들은 간단하게 Python을 이용하여 시각화했다.
물리 시스템은 두께가 10nm인 System에서 해석했다.

$$E_1 = 3.76 (meV)$$
$$E_2 = 15.04 (meV)$$
$$E_3 = 33.84 (meV)$$
$$E_4 = 60.16 (meV)$$
물론, 시각화 되지 않은 더 높은 상태들도 존재한다.
한 번더 나아가 보자.
현재 1차원에 대한 infinite potential well system을 풀었다.
이러한 System을 Quantum well (QW) system이라고 부른다.
QW system은 1차원에 대한 quantum confinement를 다룬다.
이런 QW system의 Application은 Laser, photo detector 등에 많이 사용이 된다.
물론, 실제 제작은 infinite potential well은 아니고 finite potential well에서 진행된다.
그렇다면, 2차원에 대한 infinite potential system에서는 2차원에 대한 quantum confinement effect가 나타난다.
이러한 system을 Quantum wire system 이라고 한다.
여기서 TISE에 y 변수를 추가하면 되어서 Solution의 형태도 쉽다.
(단순함을 위해, 가로 길이와 세로 길이가 같은 System을 고려했다)
$$E_n = \frac{\hbar^2 \pi^2}{2mL^2} (n_x^2+n_y^2)$$
$$\psi_{n_xn_y}(x, y) = \frac{2}{L} sin(\frac{n_x\pi x}{L})sin(\frac{n_y\pi y}{L})$$
위의 수식을 시각화한 형태는 다음과 같다.
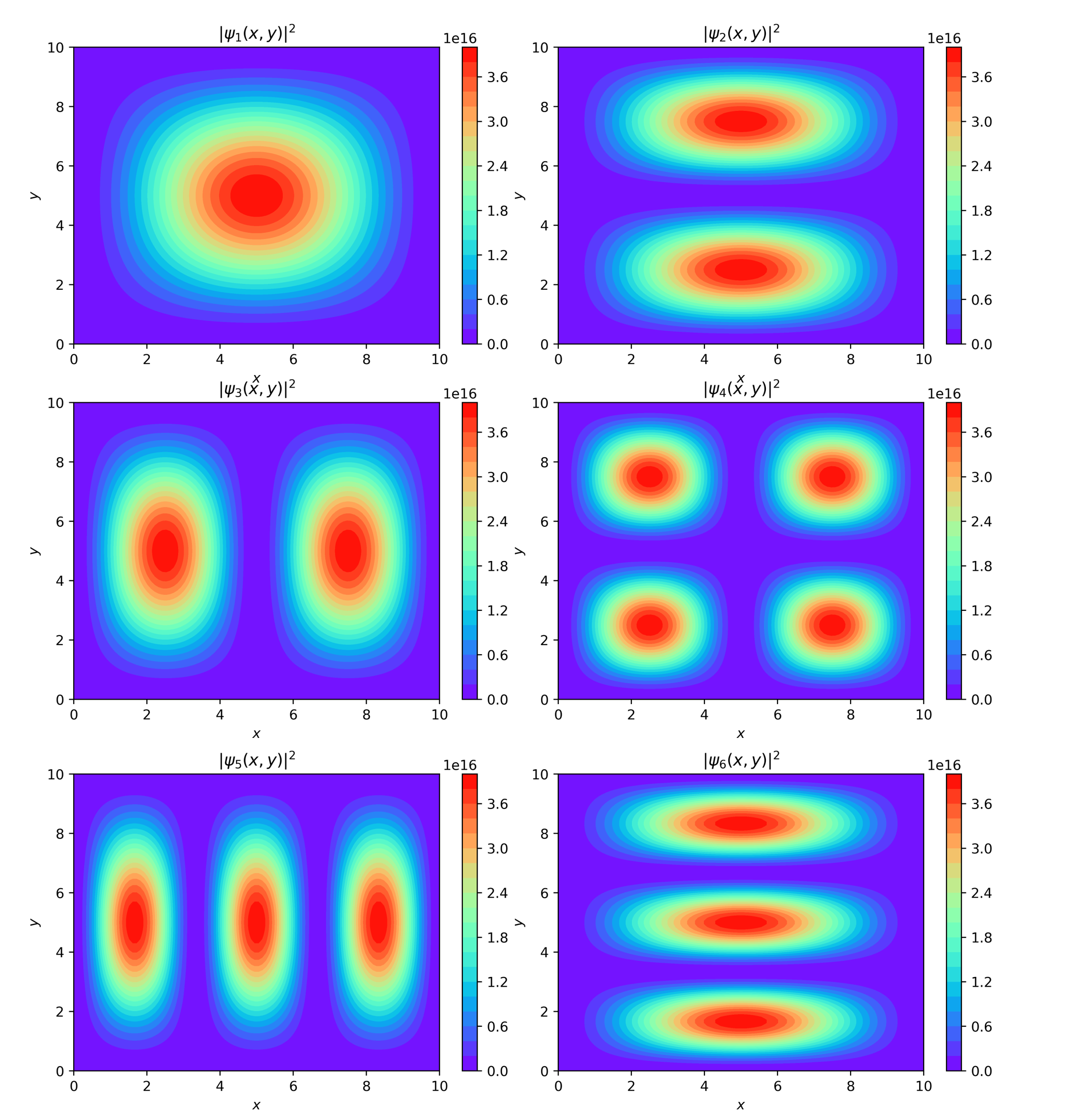
$$E_{1, 1} = 7.52 (meV)$$
$$E_{1, 2} = E_{2, 1} = 18.80 (meV)$$
$$E_{2, 2} = 30.08 (meV)$$
$$E_{1, 3} =E_{3, 1} = 37.60 (meV)$$
3차원에 대하여 Quantum confinement effect가 이뤄지는 Quantum dot system도 위와 같은 방식으로 확장이 가능하지만 시각화를 하는 것기 복잡하여 생략한다.
Discussion
위의 그림들은 Infinite potential QW 그리고 Q-Wire system들에서 전자를 발견할 확률 밀도 함수를 시각화 한 것이다.
Infinite potential well system이 우리에게 주는 기본적인 insights는 앞에서 말한 것 처럼 무한 포텐셜일 경우 입자가 존재할 확률은 0인 것과 에너지 상태가 여러개로 존재할 수 있다는 것이다.
추가적으로, 좀 더 분석해보자.
우선 파동함수를 보여준 것이 아니라 확률 밀도를 시각화하여 눈치채기 어려울 수 있다.
Infinite potential well system에서 파동함수가 sin 함수 이기때문에
odd function과 even function이 교대로 나오는 것을 알 수 있다.
그리고 자연스럽게 node가 quantum number가 증가하면서 한 개씩 증가한다.
이렇게 odd와 even functions이 교대로 나오는 이유는 parity symmetry를 만족하기 때문인데
관련해서는 나중에 정리하겠다.
다음으로 quantum number가 다른 파동함수간에 orthogonal 성질을 만족한다.
이는 파동함수가 Sin함수여서 쉽게 알 수 있다.
그리고 quantum number에 따른 계산된 에너지들은 전부 실수였다.
이것은 우리가 해석한 Hamiltonian이 Hermitian operator이기 때문이다.
Hermitian operator는 나중에 더 얘기하기로 하고 이 operator는 eigenvalue가 실수이고
eigenvector가 orthogonal하다는 성질을 가진다.
그래서, infinite potential QW이나 Q-wire도 위의 성질을 가진 것이다.
가장 중요한 insights는 ${\psi_n}$의 집합은 complete set을 만든다는 것이다.
complete set의 원소들은 System을 기술할 수 있는 basis가 되어 일반적인 물리적 상태를 기술할 수 있다.
이것도 Hermitian operator가 가지는 성질이기도 하다.
따라서, infinite potential well system에서 우리가 측정하기 전에 전자가 존재하는 상태는 다음으로 기술된다.
$$\Psi(x) = \sum_{n=1} {c_n \psi_n(x)}$$
그리고 측정을 시행하게 되면 $\psi_n$의 상태 중 하나로 붕괴 (collapse)하게 된다.
Infinite potential system에서 풀어진 상태들 중 단일 상태로 존재한다면, 해당 상태는 Stationary state를 만족한다. 다시 말해서, 확률 밀도는 시간에 대하여 변하지 않는다.
$$ \Psi(x, t) = \psi_n(x) exp(\frac{-iE_n}{\hbar}t)$$
$$|\Psi(x, t)|^2 = |\psi_n(x)|^2$$
그러나, 상태가 여러 에너지 상태들이 중첩되어 있다면 해당 물리 시스템의 확률 밀도는 시간에 대하여 evolution이 일어난다.
$$\Psi(x, t) = \psi_n(x) exp(\frac{-iE_n}{\hbar}t)+\psi_m(x) exp(\frac{-iE_m}{\hbar}t)$$
$$|\Psi(x, t)|^2 = |\psi_n(x)|^2+|\psi_m(x)|^2+2\psi_n(x)\psi_m(x)cos(\omega t)$$
마지막으로 짚어 볼 것은 Q-Wire system에서는 2개의 quantum number인 \(n_x, n_y\)로 상태를 기술했다.
여기서 나타난 현상은 에너지의 degenerate이다. (에너지가 동일한 상태)
이러한 degenerate가 일어나는 원인은 해석한 System이 symmetry를 가지기 때문이다.
이것도 추후에 깊게 다루겠다.
에너지가 degenerate가 나타나면 그 에너지 상태에 존재하는 전자는 많아 질 것이다.
그리고 여기서도 파동함수간에 orthogonal은 만족하지만 여기서는 고유에너지가 동일하기 때문에
좀 복잡해진다.
'Physics > Quantum Physics' 카테고리의 다른 글
| Finite Quantum Well 2 (0) | 2022.08.14 |
|---|---|
| Finite potential well (0) | 2022.08.04 |
| Schrodinger Equation (0) | 2022.07.21 |
| History of Quantum Mechanics (0) | 2022.07.18 |
| 양자역학 공부 시작! (0) | 2020.02.28 |





댓글